Произведение двух комплексных чисел аналогично произведению двух вещественных чисел, а именно: произведение рассматривается как число, составленное из множимого, как множитель составлен из единицы. Вектор, соответствующий комплексному числу с модулем r и аргументом j, может быть получен из единичного вектора, длина которого равна единице и направление которого совпадает с положительным направлением оси OX, путем удлинения его в r раз и поворота в положительном направлении на угол j. Произведением некоторого вектора a 1 на вектор a 2 назовём вектор, который получится, если к вектору a 1 применить удлинение и поворот, при помощи которых вектор a 2 получается из единичного вектора, причем последнему соответствует, очевидно, вещественная единица. Если (r 1 , ? 1), (r 2 , ? 2) суть модули и аргументы комплексных чисел, соответствующих векторам a 1 и a 2 , то произведению этих векторов будет, очевидно, соответствовать комплексное число с модулем r 1 r 2 и аргументом (j 1 + j 2). Таким образом, произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей и аргумент - сумме аргументов сомножителей.
В том случае, когда комплексные числа написаны в тригонометрической форме, будем иметь
r 1 (cos? 1 + i sin? 1) * r 2 (cos? 2 + i sin? 2) = r 1 r 2 .
В случае (a 1 + b 1 i)(a 2 + b 2 i) = x + yi, пользуясь обозначением модулей и аргументов сомножителей, можем написать:
a 1 = r 1 cos? 1 ; b 1 = r 1 sin? 1 ; a 2 = r 2 cos? 2 ; b 2 = r 2 sin? 2 ;
согласно определению умножения:
x = r 1 r 2 cos(? 1 + ? 2); y = r 1 r 2 sin(? 1 + ? 2),
x = r 1 r 2 (cos? 1 cos? 2 - sin? 1 sin? 2) = = r 1 cos? 1 r 2 cos? 2 - r 1 sin? 1 r 2 sin? 2 = a 1 a 2 - b 1 b 2
y = r 1 r 2 (sin? 1 cos? 2 + cos? 1 sin? 2) = = r 1 sin? 1 r 2 cos? 2 + r 1 cos? 1 r 2 sin? 2 = b 1 a 2 + a 1 b 2 ,
и окончательно получим:
(a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)i.
В случае b 1 = b 2 = 0 сомножители являются вещественными числами a 1 и a 2 и произведение приводится к произведению a 1 a 2 этих чисел. В случае
a 1 = a 2 = 0 и b 1 = b 2 = 1,
равенство (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I даёт: i???i = i 2 = -1, т.е. квадрат мнимой единицы равен -1. Вычисляя последовательно целые положительные степени i, получим:
i 2 = -1; i 3 = -i; i 4 = 1; i 5 = i; i 6 = -1; ...
и, вообще, при всяком положительном k:
i 4k = 1; i 4k+1 = i; i 4k+2 = -1; i 4k+3 = -i
Правило умножения, выражаемое равенством (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I можно формулировать так: комплексные числа надо перемножать, как буквенные многочлены, считая i 2 = -1.
Из вышеприведённых формул непосредственно следует, что сложение и умножение комплексных чисел подчиняются переместительному закону, т.е. сумма не зависит от порядка слагаемых, а произведение - от порядка сомножителей. Нетрудно проверить и справедливость сочетательного и распределительного законов, выражающихся следующими тождествами:
(? 1 + ? 2) + ? 3 = ? 1 + (? 2 + ? 3); (? 1 ? 2)? 3 = ? 1 (? 2 ? 3); (? 1 + ? 2)? = ? 1 ? + ? 2 ? .
Произведение нескольких сомножителей будет иметь модуль, равный произведению модулей сомножителей, и аргумент, равный сумме аргументов сомножителей. Таким образом, произведение комплексных чисел будет равно нулю тогда и только тогда, когда, по крайней мере, один из сомножителей равен нулю.
Пример: даны комплексные числа z 1 = 2 + 3i, z 2 = 5 - 7i. Найти:
а) z 1 + z 2 ; б) z 1 - z 2 ; в) z 1 z 2 .
а) z 1 + z 2 = (2 + 3i) + (5 - 7i) = 2 + 3i + 5 - 7i = (2 + 5) + (3i - 7i) = 7 - 4i; б) z 1 - z 2 = (2 + 3i) - (5 - 7i) = 2 + 3i - 5 + 7i = (2 - 5) + (3i + 7i) = - 3 + 10i; в) z 1 z 2 = (2 + 3i)(5 - 7i) = 10 - 17i + 15i - 21i 2 = 10 - 14i + 15i + 21 = (10 + 21) + (- 14i + 15i) = 31 + i (здесь учтено, что i 2 = - 1).
Пример: выполнить действия:
а) (2 + 3i) 2 ; б) (3 - 5i) 2 ; в) (5 + 3i) 3 .
а) (2 + 3i) 2 = 4 + 2Ч2Ч3i + 9i 2 = 4 + 12i - 9 = - 5 + 12i; б) (3 - 5i) 2 = 9 - 2Ч3Ч5i + 25i 2 = 9 - 30i - 25 = - 16 - 30i; в) (5 + 3i) 3 = 125 + 3Ч25Ч3i + 3Ч5Ч9i 2 + 27i 3 ; так как i 2 = - 1, а i 3 = - i, то получим (5 + 3i) 3 = 125 + 225i - 135 - - 27i = - 10 + 198i.
Пример: выполнить действия
а) (5 + 3i)(5 - 3i); б) (2 + 5i)(2 - 5i); в) (1 + i)(1 - i).
а) (5 + 3i)(5 - 3i) = 5 2 - (3i) 2 = 25 - 9i 2 = 25 + 9 = 34; б) (2 + 5i)(2 - 5i) = 2 2 - (5i) 2 = 4 + 25 = 29; в) (1 + i)(1 - i) = 1 2 - i 2 = 1 + 1 = 2.
В то время как сложение и вычитание комплексных чисел удобнее делать в алгебраической форме, умножение и деление проще выполнять, используя тригонометрическую форму комплексных чисел.
Возьмем два произвольных комплексных числа, заданных в тригонометрической форме:
Перемножая эти числа, получим:

Но по формулам тригонометрии

![]()
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы

складываются. Так как при этом модули преобразуются отдельно, а аргументы - отдельно, то выполнение умножения в тригонометрической форме проще, чем в алгебраической.
Из равенства (1) вытекают соотношения:

Поскольку деление - действие, обратное умножению, то при получаем, что

Иными словами, модуль частного равен отношению модулей делимого и делителя, а аргумент частного - разности аргументов делимого и делителя.
Остановимся теперь на геометрическом смысле умножения комплексных чисел. Формулы (1) - (3) показывают, что для нахождения произведения надо сначала увеличить модуль числа раз, не изменяя его аргумента, а затем увеличить аргумент полученного числа на не изменяя его модуля. Первая из этих операций геометрически означает гомотетию относительно точки О с коэффициентом , а вторая - поворот относительно точки О на угол, равный Считая здесь один множитель постоянным , а другой - переменным можем сформулировать результат так: формула
Комплексные числа - это минимальное расширение множества привычных нам действительных чисел. Их принципиальное отличие в том, что появляется элемент, который в квадрате дает -1, т.е. i, или .
Любое комплексное число состоит из двух частей: вещественной и мнимой :
Таким образом видно, что множество действительных чисел совпадает с множеством комплексных чисел с нулевой мнимой частью.
Самая популярная модель множества комплексных чисел - это обычная плоскость. Первая координата каждой точки будет её вещественной частью, а вторая -мнимой. Тогда в роли самих комплексных чисел бдут выступать вектора с началом в точке (0,0).
Операции над комплексными числами.
На самом деле, если брать в расчет модель множества комплексных чисел, интуитивно понятно, что сложение (вычитание) и умножение двух комплексных числе производятся так же как соответственные операции над векторами. Причем имеется в виду векторное произведение векторов, потому что результатом этой операции является опять же вектор.
1.1 Сложение.
(Как видно, данная операции в точности соответствует )
1.2 Вычитание , аналогично, производится по следующему правилу:
2. Умножение.

3. Деление.
Определяется просто как обратная операция к умножению.

Тригонометрическая форма.
Модулем комплексного числа z называется следующая величина:
 ,
,
очевидно, что это, опять же, просто модуль (длина) вектора {a,b}.
Чаще всего модуль комплексного числа обозначается как ρ.
Оказывается, что
z = ρ(cosφ+isinφ) .

Непосредственно из тригонометрической формы записи комплексного числа вытекают следующие формулы :
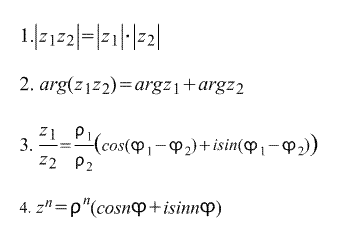
Последнюю формулу называют Формулой Муавра . Непосредственно из нее выводится формула корня n-ной степени из комплексного числа :

таким образом, существует n корней n-ной степени из комплексного числа z.
В то время как сложение и вычитание комплексных чисел удобнее делать в алгебраической форме, умножение и деление проще выполнять, используя тригонометрическую форму комплексных чисел.
Возьмем два произвольных комплексных числа, заданных в тригонометрической форме:
Перемножая эти числа, получим:

Но по формулам тригонометрии

![]()
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы

складываются. Так как при этом модули преобразуются отдельно, а аргументы - отдельно, то выполнение умножения в тригонометрической форме проще, чем в алгебраической.
Из равенства (1) вытекают соотношения:

Поскольку деление - действие, обратное умножению, то при получаем, что

Иными словами, модуль частного равен отношению модулей делимого и делителя, а аргумент частного - разности аргументов делимого и делителя.
Остановимся теперь на геометрическом смысле умножения комплексных чисел. Формулы (1) - (3) показывают, что для нахождения произведения надо сначала увеличить модуль числа раз, не изменяя его аргумента, а затем увеличить аргумент полученного числа на не изменяя его модуля. Первая из этих операций геометрически означает гомотетию относительно точки О с коэффициентом , а вторая - поворот относительно точки О на угол, равный Считая здесь один множитель постоянным , а другой - переменным можем сформулировать результат так: формула
Произведение двух комплексных чисел мы определяем аналогично произведению вещественных чисел, а именно: произведение рассматривается как число, составленное из множимого, как множитель составлен из единицы.
Вектор, соответствующий комплексному числу с модулем и аргументом может быть получен из единичного вектора, длина которого равна единице и направление которого совпадает с положительным направлением оси ОХ, путем его удлинения в раз и поворота в положительном направлении на угол
Произведением некоторого вектора на вектор назовем вектор, который получится, если к вектору применить вышеуказанные удлинение и поворот, при помощи которых вектор получается из единичного вектора, причем последнему соответствует, очевидно, вещественная единица.
Если суть модули и аргументы комплексных чисел, соответствующих векторам то произведению этих векторов будет, очевидно, соответствовать комплексное число с модулем и аргументом . Мы приходим, таким образом, к следующему определению произведения комплексных чисел:
Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей и аргумент - сумме аргументов сомножителей.
Таким образом, в том случае когда комплексные числа написаны в тригонометрической форме, будем иметь
Выведем теперь правило составления произведения для того случая, когда комплексные числа даны не в тригонометрической форме:
Пользуясь указанным выше обозначением модулей и аргументов сомножителей, можем написать
согласно определению умножения (6):

и окончательно получим
В случае сомножители являются вещественными числами и произведение приводится к произведению ахаг этих чисел. В случае равенство (7) дает
![]()
т. е. квадрат мнимой единицы равен
Вычисляя последовательно целые положительные степени , получим
и вообще, при всяком целом положительном
Правило умножения, выражаемое равенством (7), можно формулировать так: комплексные числа надо перемножать, как буквенные многочлены, считая
Если а есть комплексное число то комплексное число называется сопряженным с а, и его обозначают через а. Согласно формулам (3) имеем из равенства (7) вытекает
а следовательно,
т. е. произведение сопряженных комплексных чисел равно квадрату модуля каждого из них.
Отметим еще очевидные формулы
Из формул (4) и (7) непосредственно следует, что сложение и умножение комплексных чисел подчиняются переместительному закону, т. е. сумма не зависит от порядка слагаемых, а произведение - от порядка сомножителей. Нетрудно проверить и справедливость сочетательного и распределительного законов, выражающихся следующими тождествами:
Предоставляем сделать это читателю.
Заметим, наконец, что произведение нескольких сомножителей будет иметь модуль, равный произведению модулей сомножителей, и аргумент, равный сумме аргументов сомножителей. Таким образом, произведение комплексных чисел будет равно нулю тогда и только тогда, когда, по крайней мере, один из сомножителей равен нулю.